El mar de Fermi: ¡lo que te han contado sobre metales y electrones es mentira!
Es Lunes, 12 de la mañana, y tu yo de hace unos cuantos años (los suficientes para que estés en el instituto) se encuentra postergado en su pupitre esperando a ver qué le cuentan hoy en la asignatura de Física y Química. Pasados unos minutos el profesor da la avanzadilla: metales. Empieza explicando sus propiedades: alta densidad, brillo metálico característico, elevada maleabilidad, y especialmente una elevada conductividad eléctrica y térmica. A continuación se propone explicar el porqué de estos dos últimos aspectos, y es aquí donde el engaño se consuma.
Cuando se nos enseña qué son los metales se suele decir que son materiales en los que los átomos parecen compartir libremente todos sus electrones, formando lo que a veces se llama gas de electrones. Esta es una visión clásica, que ayuda para dar una primera idea, y que está inspirada en el comportamiento de los gases ideales. Fue desarrollada principalmente en torno a 1900, por científicos tan importantes como Drude, y aportó ideas que fueron matizadas más adelante, pero es equívoca, y para corregirla había que traer conceptos de la revolución cuántica que estaba teniendo lugar en paralelo.
Sí, yo también estoy decepcionado, los electrones han resultado no ser bolitas verdes 1 y si pensabas que ese comportamiento cuántico tan extraño que fabrica gatos zombies y partículas que se comunican entre ellas a distancia estaba sólo en los laboratorios de física atómica, prepárate que vienen curvas.
La catastrofe de la capacidad calorífica.
En primer lugar: ¿qué es la capacidad calorífica? Esto no es ni más ni menos que el nombre que damos a la energía necesaria para aumentar la temperatura de un cuerpo o sustancia en 1 grado. Como se puede deducir, esta energía dependerá de varias propiedades de la sustancia o cuerpo en cuestión, por lo que los experimentos basados en su medición (lo que da nombre al campo de la calorimetría) están muy extendidos: ¡podemos usar calorimetría para caracterizar tanto superconductores como proteínas!.
El comportamiento de la capacidad calorífica de sustancias gaseosas a finales del siglo XIX se conocía bastante bien, y se sabía que en lo que se podía enmarcar dentro de los gases ideales, la capacidad calorífica era constante (unas 6 calorías por mol de sustancia para aumentar la temperatura 1 grado). En el caso de los sólidos, después de bastante esfuerzo y gracias a las contribuciones de P Debye2 y A Einstein, se conocía que la capacidad calorífica (sin tener en cuenta los electrones) disminuía con la temperatura.
Apoyándose en este conocimiento, y considerando que los electrones de un metal se debían comportar de la misma forma que en un gas, los científicos y científicas de la época supusieron que en un metal la capacidad calorífica debería tener una contribución constante, que no dependía de la temperatura. Esto implicaría que los metales conductores deberían tener capacidades caloríficas bastante superiores a los aislantes, ya que en estos últimos no estaría presente el susodicho gas. Sin embargo, este hecho no se encuentra experimentalmente. Cuando medimos la capacidad calorífica de un sólido aislante y otro conductor, podemos observar que en realidad sus comportamientos son bastante parecidos a temperaturas bajas, siendo en realidad la contribución de los electrones directamente proporcional a la temperatura, pero… ¿por qué?
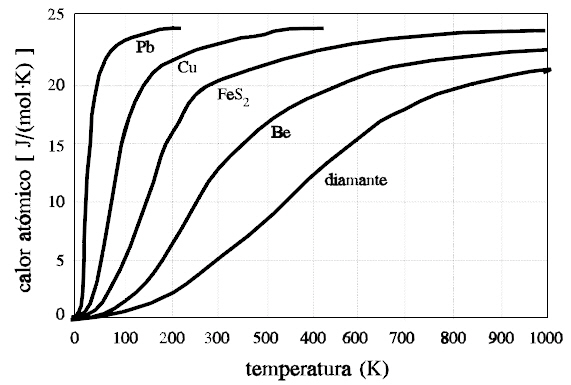
Figura 1: Ejemplo de la dependencia de la capacidad calorífica para algunos sólidos. Podemos comparar el diamante (aislante) con el cobre (Cu, metal), y ver que efectivamente sus comportamientos son similares en lo que a forma respecta. También podemos observar como a temperaturas bajas (por debajo de 100 K, lo que son unos -173 grados centígrados, todas las curvas empiezan a tomar valores muy parecidos).
Teoría cuántica para los metales: La distribución de Fermi Dirac.
Para solucionar este asunto (y otros que quedan pendientes para otro artículo) nos debemos mover al terreno de la física cuántica. Bajo este marco teórico, el movimiento y la evolución de una partícula están descritos por su estado. Este estado viene definido, en el caso de los electrones, por la energía y el momento cristalino(k), siendo la combinación de estas dos variables una especie de etiqueta que ponemos a cada electrón3.
Ambas “etiquetas” están además cuantizadas. Para entender qué significa esto comparemos una cuesta y una escalera, considerando la altura a la que nos situamos como una medida de la energía. En una cuesta podemos elegir a qué altura queremos detenernos de forma arbitraria, ya que entre dos puntos existe una variación contínua de altura (si nos encontramos a una altura de 2m, al bajar podremos pararnos en cualquier punto que queramos: 1.5m, 1.32m…). Esto representa lo que ocurre en el mundo clásico: podemos hacer variar la energía poco a poco.
Sin embargo, veamos qué ocurre en una escalera. Aquí, si los escalones tienen una cierta altura, digamos 0.2m, los únicos puntos en los que podremos detenernos serán 0, 0.2, 0.4, 0.6… ¡pero no 0.5! Es decir, existe una variación discontínua. Esto es precisamente lo que ocurre tanto con la energía como con el momento cristalino de los electrones en un metal: los valores posibles están separados por “escalones”4.
Recuperemos nuestro problema original. Cuando un conjunto de electrones libres se ve sometido a algún tipo de variación relevante en su medio (por ejemplo, un aumento en la temperatura), los electrones empezarán a cambiar de estado (en el caso de la temperatura, aumentando su energía). Y es aquí cuando todo cambia, ya que nestros electrones son fermiones, por lo que según el Principio de exclusión de Pauli dos electrones no podrán ocupar el mismo estado (es decir, no podrán compartir etiqueta). Esto implica que cuando un electrón quiere cambiar de estado no puede hacerlo a uno cualquiera, debe buscar alguna etiqueta que no esté ocupada, solo podrá evolucionar a estados vacíos. Esto explica por qué el modelo del gas de electrones no proporciona buenos resultados en cuanto a la capacidad calorífica: ¡los electrones no pueden ganar energía todos a la vez! Un electrón podrá ganar energía solo si el nivel al que quiere saltar presenta estados libres.
La forma en la que los electrones se distribuyen por niveles en un sólido sigue una distribución que se conoce como distribución de Fermi-Dirac, formando lo que a veces se llama mar de Fermi (ver Figura 2). En el sólido, todos los estados con la misma energía forman un nivel energético, por lo que el conjunto total de estados forma una estructura formada por distintos niveles. Cuando la temperatura es próxima a cero los electrones se ordenan ocupando niveles de energía de forma consecutiva, ya que no pueden ocupar todos el mismo nivel, llenando hasta una cierta energía: el nivel de Fermi. A medida que la temperatura aumenta, los electrones de los niveles más altos pueden saltar a niveles superiores que estén vacíos, y así poco a poco redistribuirse.
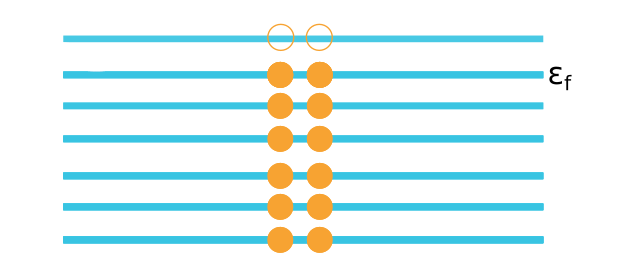
Figura 2: Esquema del mar de Fermi. Aquí hemos elegido representar únicamente dos electrones por nivel, aunque en realidad cada nivel contendrá varios valores distintos de momento cristalino.
Como esto puede ser un poco abstracto, intentemos dar un ejemplo ilustrativo. Imaginemos un centro comercial sin ascensor que se caracteriza por tener varias plantas, y en cada planta un conjunto de tiendas. En cada tienda sólo se permite la entrada a dos personas (para poder mantener así la distancia de seguridad), por lo que cada planta tiene un aforo limitado (no vale quedarse en los pasillos deambulando). En nuestro ejemplo, los estados vienen representados por planta (energía) y tienda (momento cristalino), haciendo los clientes las de electrones. Los protocolos de seguridad juegan el papel del Principio de exclusión de Pauli5. Este símil resulta conveniente porque las tiendas se reparten en el espacio, al igual que los valores de momento cristalino k en realidad se representan por vectores de componentes (kx ,ky,kz), siendo por tanto puntos en un espacio tridimensional que llamamos espacio recíproco o sipmlemente espacio k. Esto implica que en realidad la distribución que hemos representado en la Figura 2 tome forma esférica en dicho espacio (ver Figura 3). La próxima vez que hablemos de metales esto será relevante, pero de momento sigamos con nuestro centro comercial.
Figura 3: En realidad, el momento cristalino k se trata de un vector con componentes (kx ,ky,kz). El diagrama que hemos representado antes toma entonces una forma esférica, siendo la última capa lo que se conoce como superficie de Fermi, que lleva asociada la energía correspondiente al nivel de Fermi. Los niveles energéticos tienen ahora formas de esferas que están contenidas dentro de la esfera de Fermi.
Llegan las 8 de la mañana, y la gente empieza a entrar en el centro comercial. Al principio, la gente intenta quedarse en las tiendas de la planta baja (al fin y al cabo, a nadie le gusta subir escaleras). Sin embargo, cuando la primera planta ha llenado el aforo, las personas que entren deben subir a la siguiente. Esto supone un ordenamiento similar al que ocurre en la Figura 2.
Ahora supongamos que el aire acondicionado de este extraño centro comercial se encuentra en la última planta, y que una terrible ola de calor acecha a nuestros ordenados consumidores. Las personas que estén comprando en la última planta intentarán ir a la planta inmediatamente superior, donde la temperatura es más reconfortante6. Sin embargo, ¿qué ocurre si uno de los clientes de las plantas inferiores intenta ascender? ¡No puede! Debe esperar a que las personas de plantas superiores se muevan para que el aforo no esté completo, lo que le permitirá moverse y alcanzar su deseado frescor.
Conclusiones
¿Es esto todo? ¿Podemos volver a dormir tranquilos? El modelo que hemos descrito aquí se conoce como Modelo de electrones casi libres. Tanto el modelo en sí como la distribución de Fermi-Dirac fueron grandes pasos que dió la física de la materia condensada a principios del siglo XX, pero aún quedaban muchos problemas sin resolver. Los datos de conductividad que se esperaban siguiendo este modelo para algunos materiales parecían ser bastante mayores a los medidos en el laboratorio, incluso aplicando las ideas de Fermi y Dirac, ¿qué estaba ocurriendo?. Siguiendo a esta pregunta cabía ir más allá: ¿por qué existen sólidos metálicos y sólidos aislantes? Muchas sorpresas estarían aún por llegar, todas ellas de la mano de la física cuántica, dando lugar a un escenario de nuevas ideas y conceptos que aún hoy sigue creciendo.
1: O azules, el eterno debate.↩
2: Dato curioso: El físico Peter Debye nació en Maastrich (Países Bajos) en 1912, y por ende su nombre originalmente era Petrus Debije. Posteriormente se mudaría a EEUU y se cambiaría el nombre al recibir la nacionalidad, siendo los motivos todavía objeto de debate y mucha controversia. Lo interesante es que aún hoy en las universidades neerlandesas puede oirse a los profesores usar su nombre original (y leerse en la bibliografía en neerlandés).↩
3: El momento cristalino es en muchos casos proporcional al momento lineal y por tanto, podemos pensar en él como una cantidad relacionada con la velocidad de los electrones. Nota avanzada: Esto tiene matices sutiles. El operador momento lineal aplicado a las funciones de onda de los electrones en sólidos no es únicamente proporcional al momento cristalino, existe un término más que evita relacionarlos directamente. Este símil surge del comportamiento de los electrones bajo la aplicación de campos eléctricos, en lo que se conoce como teoría semiclásica para la conducción. Puede encontrarse más en Ashcroft & Mermin Ch 8.↩
4: ¿Por qué ocurre esto? Las cuerdas de una guitarra no pueden vibrar de cualquier forma, ya que sus extremos deben mantenerse siempre fijos (a menos que quieramos que nuestro pobre guitarrista sufra un accidente). Esto da lugar a que las formas de vibrar (modos de vibración) estén también cuantizados en una cuerda, lo que llamamos normalmente ondas estacionarias. De forma similar podemos pensar que nuestros electrones se describen ahora como ondas, que al estar confinadas en el volumen que delimita el metal tienen que cumplir condiciones parecidas a las de la cuerda de guitarra, dando lugar a modos de vibración cuantizados. Nota avanzada: Lo que ocurre es que la función de onda de los electrones debe cumplir la condición de anularse en las fronteras del metal. La razón es que si la función de onda (módulo al cuadrado) representa la probabilidad de encontrar el electrón, debemos forzar que la probabilidad de que el electrón escape del metal de forma espontánea sea nula. ↩
5: Cada estado de energía y momento cristalino puede estar ocupado por dos electrones porque estos, al tener diferente espín, ocupan en realidad estados distintos. Esto es algo que se sobreentiende en el contexto de la física del estado sólido, por lo que para caracterizar los estados no se suele usar también el espín.↩
6: No van a intentar ir a la última planta porque recordemos: nuestros clientes son esencialmente vagos, y no quieren subir demasiadas escaleras.↩
Referencias
[1]: Wikimedia Commons[https://commons.wikimedia.org/wiki/File:Moglft0304_calor_solidos.jpg] (visita 25/11/2020)
[2]: Hyperphysics [http://hyperphysics.phy-astr.gsu.edu/hbasees/Solids/Fermi.html] (visita 25/11/2020)
[3]: Ashcroft, N. and Mermin, N. (1976) Solid State Physics. Harcourt Brace College Publishers, New York.